Values representation

1 Introduction

One decision that must be taken when designing a compiler is how to represent the values of the source language in the target language.

For simple languages, this is almost trivial to do as the type of all values is known by the compiler, and these types have a direct correspondence in the target language. For example, in C, the type of all values is known at compilation time, and these values — integers, floating point numbers, etc. — are directly representable on a typical processor.

For higher-level, and/or more dynamic languages, the problem is trickier for two reasons:

the exact type of some values might not be known at compilation time,
some values might not be easily representable in the target language.

As an example, consider the following L₃ function:

(def pair-make
  (fun (f s)
    (let ((p (@block-alloc-0 2)))
      (@block-set! p 0 f)
      (@block-set! p 1 s)
      p)))

Obviously, the L₃ compiler knows nothing about the type of the values that will be passed as arguments to this function at run time. Therefore, all values must be represented in a uniform fashion, to ensure that a function like the one above can be compiled without knowing the type of the values being manipulated.

Notice that this problem is not specific to dynamically-typed languages like L₃. It also exists in statically-typed languages that offer parametric polymorphism, like Scala, in which a function very similar to the one above can be written:

def pairMake[T,U](f: T, s: U): Pair[T,U] =
  new Pair[T,U](f, s)

We will call values (or data) representation the problem of deciding how to (efficiently) represent the values of the language being compiled.

2 Representation strategies

Several strategies exist to solve the values representation problem, each with their pros and cons. The most common one are described in the following sections.

2.1 Boxing

Probably the simplest way to represent values uniformly is to box them.

Boxing consists in representing all source values by a pointer to a heap-allocated block, often called a box. That block contains the representation of the source value, as well as a tag identifying the type of that value.

While simple, this technique is costly, as even small values like integers or booleans are stored in the heap. Basic operations like integer addition require fetching the integers to add from their box, adding them and storing the result in a newly-allocated box.

2.2 Tagging

A solution to avoid paying the hefty price of boxing for small values like integers, booleans, etc. is to tag them.

Like boxing, tagging consists in representing all values uniformly by a machine word, but this word can contain either:

a pointer to a boxed value, as before, or
a value that is small enough to fit in (a part of) the word.

The two cases are distinguished using some of the bits of the word. For example, heap-allocated blocks are usually allocated at addresses aligned on multiples of 2, 4 or more addressable units. This implies that some of the least significant bits of their address are always zero. Provided that tagged values are represented in such a way that some of these bits are different from zero, it is possible to distinguish them from pointers.

2.2.1 Integer tagging

A popular tagging strategy consists in representing the source integer n as the target integer 2n+1. This ensures that the least significant bit of the target integer is always 1, which makes it distinguishable from pointers at run time.

The drawback of this encoding is that the source integers have one bit less than the integers of the target architecture. While rarely a problem, some programs can become cumbersome to write in such conditions — e.g. the computation of a 32 bits checksum.

For that reason, some languages like OCaml offer several kinds of integer-like types: fast, tagged integers with reduced range, and slower, boxed integers with the full range of the target architecture.

2.2.2 NaN tagging

With the current move towards 64 bits architectures, it can make sense to use 64 bits words to represent values. Although a tagging scheme similar to the one described above can also be used in this case, an alternative based on 64 bits floating-point values exists.

The IEEE 754 standard defining the format of the 64 bits floating-point values used in most languages (e.g. double in Java or C) uses a surprisingly large subset of all 64 bits values to represent errors. These values, called not-a-number (NaN), are produced by operations whose result is undefined, e.g. when dividing 0 by 0. They are identified by their 12 most significant bits, which must all be 1, while the remaining 52 bits can carry an arbitrary payload.

This characteristic can be used to represent all values uniformly as a 64 bits word containing either:

a valid, non-NaN IEEE 754 floating-point value, or
a pointer, integer, character, etc. stored in the payload of a NaN.

This is colloquially known as NaN tagging and is used in several Javascript implementations.

2.3 On-demand boxing

Statically-typed languages have the option of using unboxed/untagged values for monomorphic code, and switching to (and from) boxed/tagged representation only for polymorphic code. This is what Java and Scala do, for example.

Dynamically-typed language implementations can try to infer types to obtain the same result, although this is generally only doable in the context of dynamic (JIT) compilation.

2.4 Specialization

For statically-typed, polymorphic languages, specialization (or monomorphization) is another way to represent values.

Specialization consists in translating polymorphism away by producing several specialized versions of polymorphic code. For example, when the type List[Int] appears in a program, the compiler produces a special class that represents lists of integers — and of nothing else. This is what Rust and C++ do, for example.

Full specialization removes the need for a uniform representation of values in polymorphic code. However, this is achieved at a considerable cost in terms of code size. Moreover, the specialization process can even fail to terminate in cases like the following:

class C[T]
class D[T] extends C[D[D[T]]]

2.5 Partial specialization

To reap some of the benefits of specialization without paying its full cost, it is possible to perform partial specialization.

For example, since in Java all objects are manipulated by reference, there is no point in specializing for more than one kind of reference (e.g. String and Object).

It is also possible to generate specialized code only for types that are deemed important — e.g. double in a numerical application — and fall back to non-specialized code, with a uniform representation, for the other types. This is what Scala's @specialized annotation allows, for example.

2.6 Comparing strategies

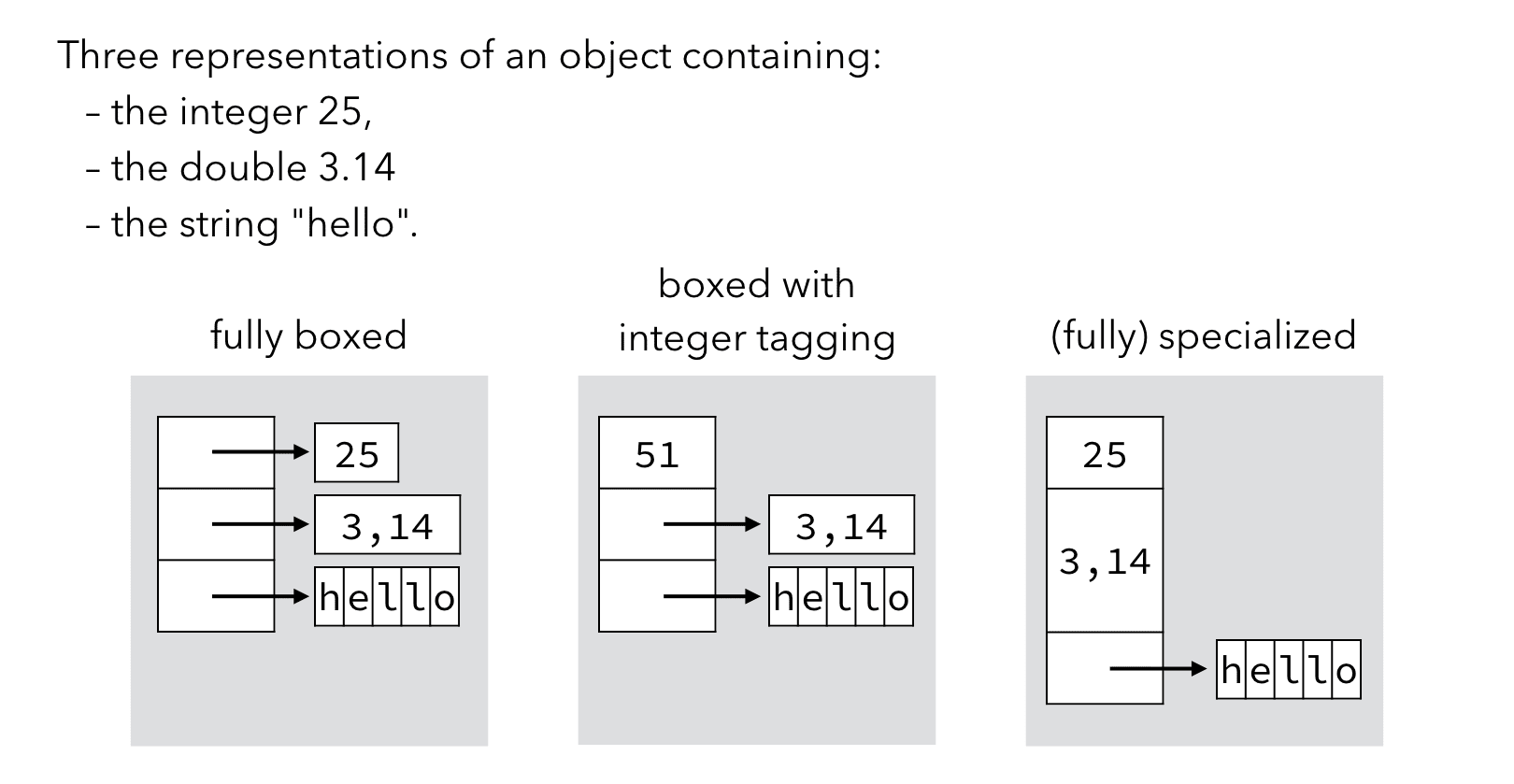
The image below compares a few of the strategies presented earlier on a simple example.

2.7 Translation of operations

When a source value is encoded to a target value, the operations on the source values have to be compiled according to the encoding.

For example, if integers are boxed, the addition of two source integers has to be compiled as the following sequence:

the two boxed integers are unboxed,
the sum of these unboxed values is computed, and
a new box is allocated and filled with that result.

This new box is the result of the addition.

Similarly, if integers are tagged, the tags must be removed before the addition is performed, and added back afterwards — at least in principle. It is however possible to do better for several operations, as the table below illustrates. It shows how the encoded version of three basic arithmetic primitives can be derived for tagged integers:

Similar derivations can be made for other operations (division, remainder, bitwise operations, etc.).

3 L₃ values representation

As a reminder, L₃ has the following kinds of values: tagged blocks, functions, integers, characters, booleans and unit.

In our implementation, tagged blocks are represented as pointers to themselves. Since they are aligned on multiples of 4 bytes, the two least significant bits of their address are always 0. This makes it possible to use the following tagging scheme to represent integers, characters, booleans and the unit value:

Kind of value	LSBs
Integer	…1
Block (pointer)	…00
Character	…110
Boolean	…1010
Unit	…0010

For now, we will assume that functions are represented as pointers to their first instruction, although we will see later that this is insufficient.

3.1 Values representation phase

The values representation phase of the L₃ compiler takes as input a CPS/L₃ program where all values and primitives are "high-level", in that they have the semantics of the L₃ language gives them. It produces a "low-level" version of that program as output, in which all values are bit vectors (integers or pointers) and primitives correspond directly to the instructions of the virtual machine, which are close to those of a typical processor.

As usual, this phase is specified as a transformation function called ⟦·⟧, which maps high-level CPS/L₃ terms to their low-level equivalent. This function is given below: