Closure conversion

All mainstream programming languages offer a notion of function. However, they are often not "first-class citizens", in that what one can do with them is more restricted than with other kinds of values.

For example, in C it is possible to pass a function as an argument, and to return a function as a result. However, C functions cannot be nested and must all appear at the top level. This severely restricts their usefulness, but greatly simplifies their implementation as they can be represented as simple code pointers.

In functional languages — Scala, OCaml, Haskell, etc. — functions can be nested, and they can survive the scope that defined them. This is very powerful as it permits the definition of functions that return "new" functions, e.g. a function that returns the composition of two other functions. However, it also complicates the representation of functions, as simple code pointers are no longer sufficient.

To illustrate the issues related to the representation of functions in a functional language, consider the following L₃ example:

(def make-adder
  (fun (x)
    (fun (y) (@+ x y))))
(def increment (make-adder 1))
(increment 41) ; ⇒ 42
(def decrement (make-adder -1))
(decrement 42) ; ⇒ 41

The functions returned by make-adder can basically be represented using two strategies:

1. using simple code pointers, which implies run-time code generation as each function returned by make-adder is different,
2. using another representation, which does not depend on run-time code generation.

To adequately represent the functions returned by make-adder, their code pointer must be augmented with the value of x.

Such a combination of a code pointer and an environment giving the values of the free variable(s) — here x — is called a closure. The name refers to the fact that the pair composed of the code pointer and the environment is closed, i.e. self-contained.

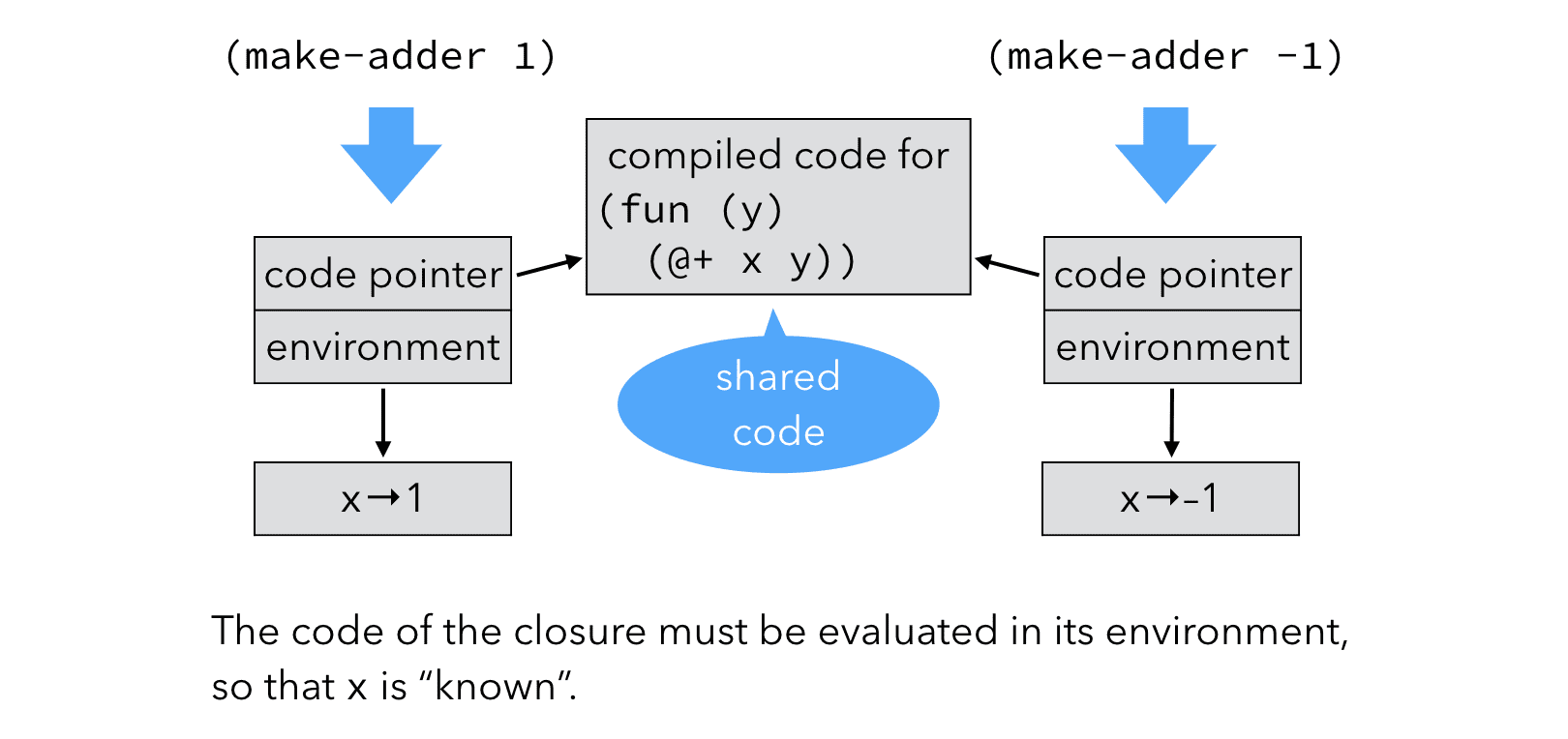
Using closures instead of function pointers changes the way functions are manipulated at run time:

• function abstraction builds and returns a closure instead of a simple code pointer,
• function application extracts the code pointer from the closure, and invokes it with the environment as an additional argument.

Notice that when compiling function application, in the general case nothing is known about the closure being applied: it could be any one of those defined in the program. Therefore, the code pointer has to be at a known and constant location, so that it can be extracted. On the other hand, the values contained in the environment are not used during application itself: they will only be accessed by the function body. This provides some freedom to place them.

In particular, it is possible to represent closures not as a pair of (code, environment) pointers, but as a block whose first slot contains the code pointer, and the other slots (if any) contain the free variables. This saves memory and is more efficient, due to the removal of one indirection. Such closures are known as flat closures.

In a compiler, closures can be implemented by a simplification phase called closure conversion.

Closure conversion transforms a program in which functions can have free variables into an equivalent one containing only closed functions. The output of closure conversion is therefore a program in which functions can be represented as code pointers.

Notice that closure conversion is nothing more than values representation for functions: it encodes the high-level notion of functions of the source language using the low-level concepts of the target language — in this case heap-allocated blocks and code pointers.

The L₃ compiler represents L₃ functions using flat closures stored in blocks tagged with a tag reserved for them (202). The first element of the block contains the code pointer while the other elements — if any — contain the environment of the closure.

Closure conversion is not a separate phase in the L₃ compiler. Rather, it is the part of the values representation phase that takes care of representing function values. It is therefore specified exactly like the values representation phase.

Before specifying it, we need to define an auxiliary function to compute the set of free variables of a function:

Closure conversion must only handle two constructs: function abstraction and function application.

Function abstraction is transformed as follows. Notice that this rule is meant to replace the temporary, incorrect one presented in the lecture about values representation:

Function application is transformed as follows. Like the one for function abstraction, this rule is meant to replace the temporary and incorrect one presented in the previous lecture:

Notice that since functions are represented as tagged blocks, checking that an arbitrary object is a function amounts to checking that it is a tagged block and if it is, that its tag is 202. This can be done directly in L₃, as a library function:

(def function?
  (fun (o)
    (and (@block? o)
         (@= 202 (@block-tag o)))))

This is the reason why L₃ does not include a function? primitive.

The translation just presented is suboptimal in two respects:

1. it always creates closures, even for functions that are never used as values (i.e. only applied),
2. it always performs calls through the closure, thereby making all calls indirect.

These problems could be solved by later optimizations or by a better version of the translation, sketched below.

The inefficiency of the simple translation can be observed on the make-adder example:

(def make-adder
  (fun (x)
    (fun (y) (@+ x y))))
(make-adder 1)

Applied to the CPS/L₃ version of that program, the simple translation creates a closure for both functions. However, the outer one is closed and never used as a value, therefore no closure needs to be created for it.

Notice that even if the outer function escaped (i.e. was used as a value) and needed a closure, the call to it could avoid fetching its code pointer from the closure, as here it is a known function.

Improving the translation requires translating a single source function into two target functions — instead of one — and one closure. These two functions are:

1. the wrapper, which simply extracts the free variables from the environment and passes them as additional arguments to the worker,
2. the worker, which takes the free variables as additional arguments and does the real work.

The wrapper is put in the closure. The worker is used directly whenever the source function is applied to arguments instead of being used as a value. The rule for function translation therefore becomes:

while the one for function application becomes:

Notice that the improved translation makes the computation of free variables slightly more difficult. That's because when a function f calls a known function g, it has to pass it its free variables as additional arguments. The free variables of g now become free variables of f. These new free variables must be added to f's arguments, which impacts its callers — which could include g if the two are mutually-recursive. And so on…

After closure conversion, all functions in the program are closed. Therefore, it is possible to hoist them all to a single outer letf. Once this is done, the program has the following simple form:

(letf (…) ; all functions of the program
  ; main program code, not containing any function definition
  )

In other words, the program contains exactly one letf, at the root of the tree, defining all the functions of the program.

Hoisting functions to the top level simplifies the shape of the program and can make the job of later phases — e.g. assembly code generation — easier. It is specified by the rules below:

There is a strong similarity between closures and objects: closures can be seen as objects with a single method — containing the code of the closure — and a set of fields — the environment.

Anonymous nested classes can therefore be used to simulate closures, but the syntax for them is often too heavyweight to be used often. In languages like Scala or Java 8, a special syntax exists for anonymous functions, which are translated to nested classes, conceptually at least.

To see how closures are handled in Scala, let's look at how the Scala equivalent of the make-adder function:

def makeAdder(x: Int): Int => Int =
  { y: Int => x+y }
val increment = makeAdder(1)
increment(41)

is translated:

(Notice that this translation might not correspond to the one done by the latest version of the compiler, but it is equivalent.)