Instruction scheduling
1 Introduction
When a compiler emits the instructions corresponding to a program, it imposes a total order on them. However, that order is usually not the only valid one, in the sense that it can be changed without modifying the program's behavior. For example, when two successive instructions are independent, it is possible to swap them.
Among all the valid permutations of the instructions composing a program — i.e. those that preserve the program's behavior — some can be more desirable than others. For example, one might lead to a faster program on some machine, because of architectural constraints.
The aim of instruction scheduling is to find a valid order that optimizes some metric, like execution speed.
On modern, pipelined architectures, this is achieved by ordering the instructions in such a way that pipeline stalls are avoided as much as possible. These stalls are due to instruction operands not being available at the time the instruction is executed, e.g. because their computation is not finished yet or because they have to be fetched from memory.
1.1 Example
The following example will illustrate how proper scheduling can reduce the time required to execute a piece of RTL code. We assume the following delays for instructions:
| Instruction kind | RTL notation | Delay |
|---|---|---|
| Memory load or store | Ra <- Mem[Rb + c] | 3 |
| Multiplication | Ra <- Rb * Rc | 2 |
| Addition | Ra <- Rb + Rc | 1 |
The image below shows two versions of the same program: the left one is what could be generated by a compiler that is not doing any scheduling, while the right one is a properly scheduled one.
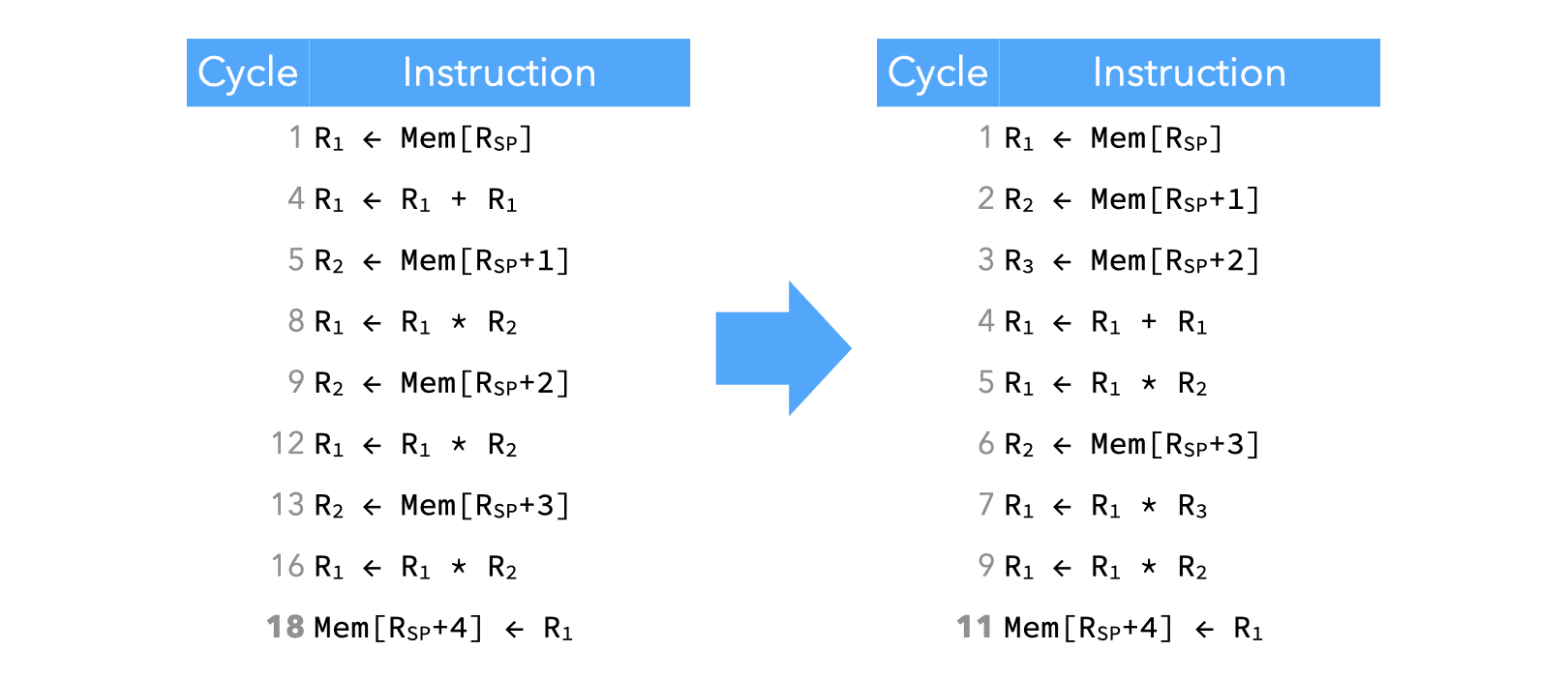
The effect of scheduling is quite dramatic here, as it allows the last instruction to be issued at cycle 11 instead of cycle 18.
2 Dependencies
An instruction i2 is said to depend on an instruction i1 when it is not possible to execute i2 before i1 without changing the behavior of the program.
The most common reason for dependence is data-dependence: i2 uses a value that is computed by i1. This is known as a true dependency, but two additional kinds of dependencies exist, known as anti-dependencies.
Therefore, a total of three different kinds of dependencies exist:
- true dependence — i2 reads a value written by i1 (read after write or RAW),
- anti-dependency — i2 writes a value read by i1 (write after read or WAR),
- anti-dependency — i2 writes a value written by i1 (write after write or WAW).
Anti-dependencies are not real dependencies, in the sense that they do not arise from the flow of data. They are due to a single location being used to store different values. Most of the time, they can be removed by "renaming" locations, e.g. using a different register.
For example, the program on the left below contains a WAW anti-dependency between the two memory load instructions. It can be removed by "renaming" the second use of R1 in the last two instructions, and using R2 instead.
| Original | Renamed |
|---|---|
| R1 <- Mem[Rsp] | R1 <- Mem[Rsp] |
| R4 <- R4 + R1 | R4 <- R4 + R1 |
| R1 <- Mem[Rsp + 1] | R2 <- Mem[Rsp + 1] |
| R4 <- R4 + R1 | R4 <- R4 + R2 |
Identifying dependences among instructions that only access registers is easy. Instructions that access memory are harder to handle since it is not possible, in general, to know whether two such instructions refer to the same memory location. Conservative approximations therefore have to be used, but we will not cover them here.
2.1 Dependence graph
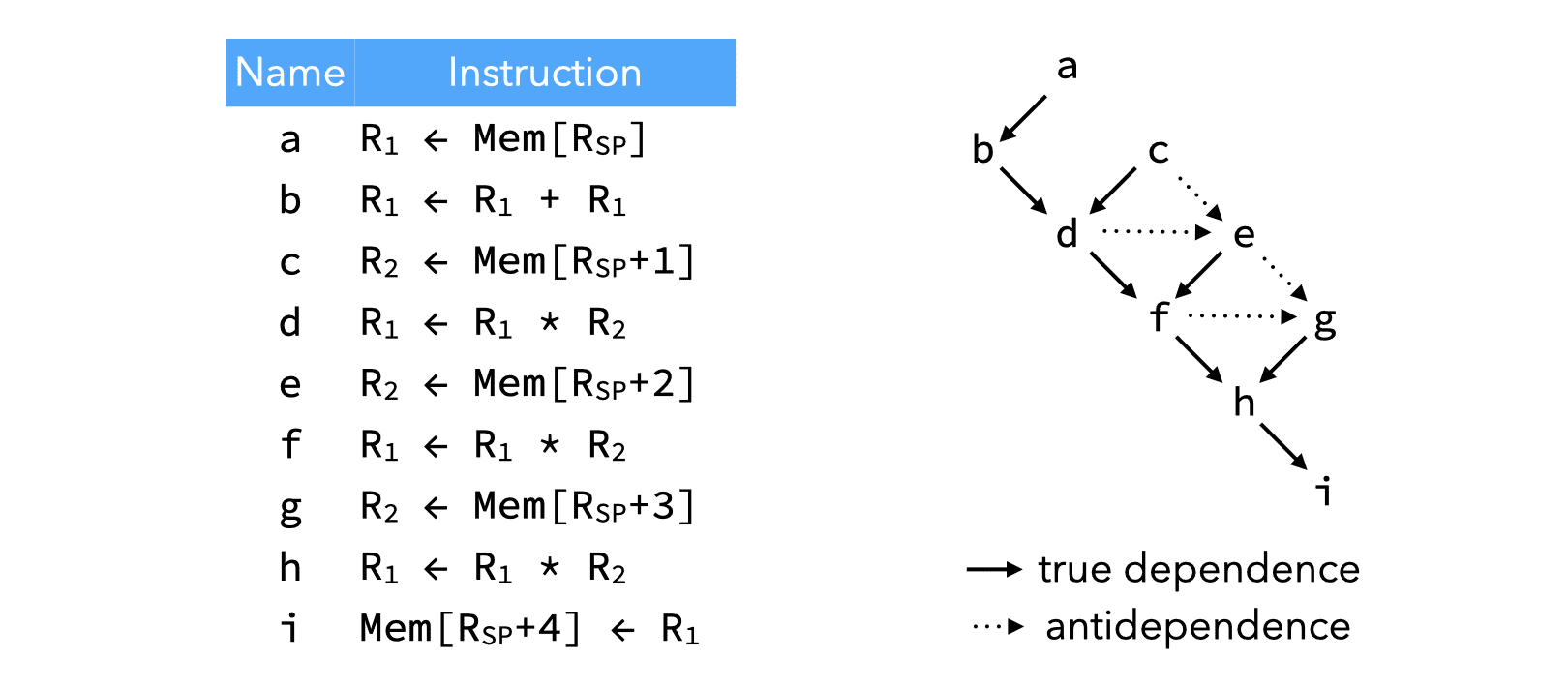
The dependence graph is a directed graph representing dependences among instructions. Its nodes are the instructions to schedule, and there is an edge from node n1 to node n2 iff the instruction of n2 depends on that of n1. Any topological sort of the nodes of this graph represents a valid way to schedule the instructions.
The image below shows the dependence graph for the example program presented earlier.
3 List scheduling
Optimal instruction scheduling is NP-complete. As usual, this means that heuristics have to be used to try to find a good, but usually not optimal, solution to that problem.
List scheduling is such a heuristic technique to schedule the instructions of a single basic block. Its basic idea is to simulate the execution of the instructions, and to try to schedule instructions only when all their operands are ready. To do this, it maintains two lists:
readyis the list of instructions that could be scheduled without stall, ordered by priority (see below),activeis the list of instructions that are being executed.
At each step, the highest-priority instruction from ready is scheduled, and moved to active, where it stays for a time equal to its delay. Notice that before scheduling is performed, renaming is done to remove all anti-dependencies that can be removed.
Several notions of priority can be used to order the instructions of the ready list, but unfortunately none of them gives the best results in all cases. The most commonly-used notions for the priority of a node (i.e. of an instruction) are:
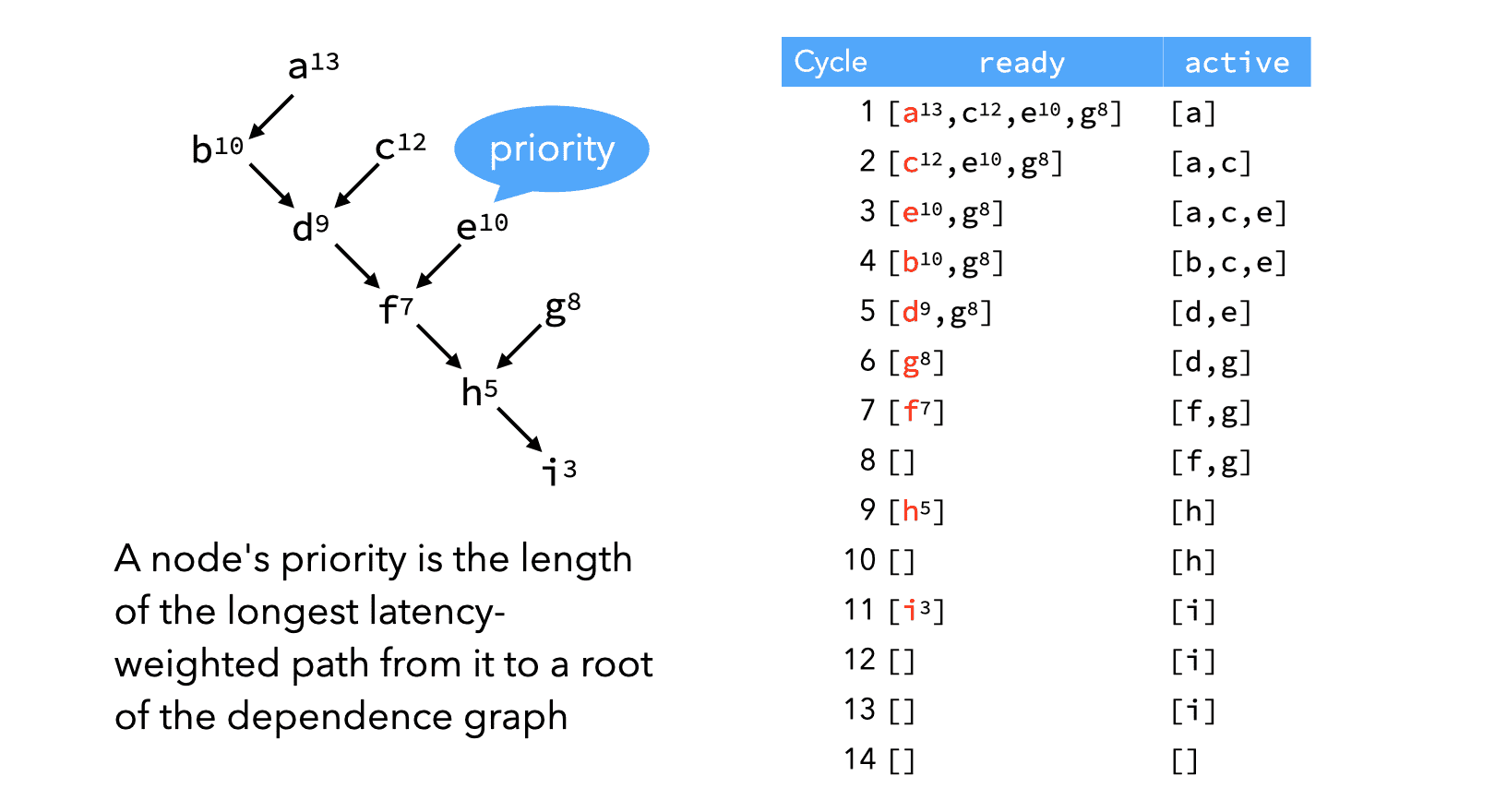
- the length of the longest latency-weighted path from it to a root of the dependence graph,
- the number of its immediate successors,
- the number of its descendants,
- its latency,
- etc.
3.1 Example
The image below (available as an animation in the lecture slides) shows how list scheduling can be applied to our example.
4 Scheduling vs register allocation
It is hard to decide whether scheduling should be done before or after register allocation: on the one hand, if register allocation is done first, it can introduce anti-dependencies when reusing registers; on the other hand, if scheduling is done first, register allocation can introduce spilling code, destroying the schedule.
The usual solution is to schedule first, then allocate registers, and finally schedule once more if spilling was necessary.