Tail calls
1 Introduction
Several functional programming languages do not have an explicit looping statement. Instead, programmers resort to recursion to loop. For example, the central loop of a Web server written in L3 might look like this:
(defrec web-server-loop
(fun ()
(wait-for-connection)
(fork handle-connection)
(web-server-loop)))
Unfortunately, recursion is not equivalent to the looping statements usually found in imperative languages: recursive function calls, like all calls, consume stack space while loops do not. In our example, this means that the Web sever will eventually crash because of a stack overflow. This is clearly unacceptable, and a solution to that problem must be found.
In this example, it is obvious that the recursive call to web-server-loop could be replaced by a jump to the beginning of the function. If the compiler could detect this case and replace the call by a jump, the problem would be solved.
2 Tail calls
The reason why the recursive call of web-server-loop could be replaced by a jump is that it is the last action taken by the function. Calls that appear in terminal position like this one are called tail calls. This particular tail call also happens to be recursive, and is therefore said to be a recursive tail call. Notice however that tail calls do not have to be recursive (this is a common misconception).
When a function performs a tail call, its own activation frame is dead, as by definition nothing follows the tail call. Therefore, it is possible to first free the activation frame of a function about to perform such a call, then load the parameters for the call, and finally jump to the called function's code.
This technique is called tail call elimination (or optimization), here abbreviated TCE.
3 Tail call elimination
Consider the following function definition and call:
(defrec sum
(fun (z l)
(if (list-empty? l)
z
(sum (+ z (list-head l))
(list-tail l)))))
(sum 0 (list-make-3 1 2 3))
The recursive call to sum is a tail call, and tail call elimination can therefore be performed on it.
The following image illustrates how the stack would evolve during the execution of the above program fragment in the absence of tail call elimination:
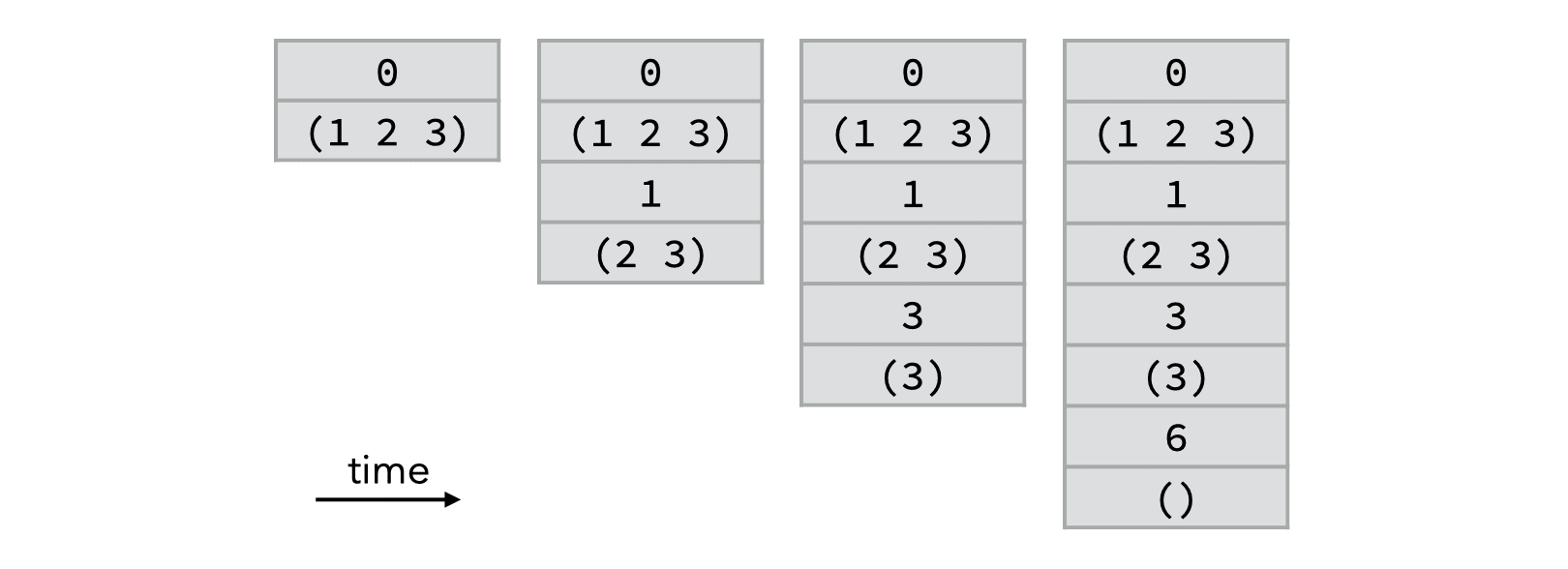
while the following one illustrates how the stack would evolve in presence of tail call elimination:

Notice that tail call elimination is more than just an optimization. Without it, writing a program that loops endlessly using recursion and does not produce a stack overflow is simply impossible.
For that reason, full tail call elimination is actually required in some languages, e.g. Scheme. In other languages, like C, it is simply an optimization performed by some compilers in some or all cases.
4 Tail calls in L3
The "simple" translation from CL3 to CPS/L3 does not handle tail calls specially, and their translation is therefore sub-optimal. For example, as we have seen, the CL3 term:
(letrec ((f (fun (g) (g)))) f)
gets translated to the CPS/L3 term:
(letf ((f (fun (r1 g) (letc ((r2 (cnt (v) (appc r1 v)))) (appf g r2))))) f)
in which the tail call from f to g returns to f — since its return continuation is r2 — instead of directly returning to its caller.
On the other hand, the improved translation from CL3 to CPS/L3 does handle tail calls specially, and optimizes them correctly. With it, the same CL3 term as before gets translated to the CPS/L3 term:
(letf ((f (fun (r1 g) (appf g r1)))) f)
in which the tail call to g is optimized, in that it gets the same return continuation r1 as f itself. This is due to the fact that the improved translation uses a different translation function — called tail — for terms that are in tail position.
It is worth comparing how the two translation functions (nonTail and tail) differ in their translation of function application:

Finally, notice that in the L3 compiler, CPS/L3 is just an intermediate language, not the final target language. Therefore, when translating CPS/L3 to virtual machine code, tail calls must be identified and translated appropriately. However, given how they are handled by the improved translation function, their identification is trivial: a CPS/L3 function call is a tail call iff it gets the return continuation of its enclosing function.
5 TCE in uncooperative environments
When generating assembly language, it is easy to perform TCE, as the target language is sufficiently low-level to express the deallocation of the activation frame and the following jump.
When targeting higher-level languages, like C or the JVM, this becomes difficult — although recent VMs like .NET's support tail calls. It is therefore interesting to explore techniques that can be used to perform TCE in such uncooperative environments.
To illustrate how the various techniques work, we will use an example program in C that tests whether a number is even, using two mutually tail-recursive functions. When no technique is used to manually eliminate tail calls, it looks as follows:
int even(int x) {
return x == 0 ? 1 : odd(x-1);
}
int odd(int x) {
return x == 0 ? 0 : even(x-1);
}
int main(int argc, char* argv[]) {
printf("%d\n", even(300000000));
}
Unless the C compiler performs TCE — like GCC or clang do with full optimization — this program crashes with a stack overflow at run time.
5.1 Single function
The single function approach consists in compiling the whole program to a single function of the target language. This makes it possible to compile tail calls to simple jumps within that function, and other calls to recursive calls to it.
This technique is rarely applicable in practice, due to limitations in the size of functions of the target language.
Using this technique, our example program could be rewritten as follows:
typedef enum { fun_even, fun_odd } fun_id;
int wholeprog(fun_id fun, int x) {
switch (fun) {
case fun_even: goto even;
case fun_odd: goto odd;
}
even:
if (x == 0) return 1;
x = x - 1;
goto odd;
odd:
if (x == 0) return 0;
x = x - 1;
goto even;
}
int main(int argc, char* argv[]) {
printf("%d\n", wholeprog(fun_even, 300000000));
}
5.2 Trampolines
With trampolines, functions never perform tail calls directly. Rather, they return a special value to their caller, informing it that a tail call should be performed. The caller performs the call itself, on their behalf.
For this scheme to work, it is necessary to check the return value of all functions, to see whether a tail call must be performed. The code which performs this check is called a trampoline.
Using such a trampoline, our example program could be rewritten as follows:
typedef void* (*fun_ptr)(int);
struct { fun_ptr fun; int arg; } resume;
void* even(int x) {
if (x == 0) return (void*)1;
resume.fun = odd;
resume.arg = x - 1;
return &resume;
}
void* odd(int x) {
if (x == 0) return (void*)0;
resume.fun = even;
resume.arg = x - 1;
return &resume;
}
int main(int argc, char* argv[]) {
void* res = even(300000000);
while (res == &resume) /* the trampoline */
res = (resume.fun)(resume.arg);
printf("%d\n",(int)res);
}
5.3 Extended trampolines
Extended trampolines trade some of the space savings of standard trampolines for speed.
The idea is that instead of returning to the trampoline on every tail call, the number of successive tail calls is counted at run time, using a tail call counter passed to every function. Then, when that number reaches a predefined limit, a non-local return is performed to transfer control to a trampoline "waiting" at the bottom of the chain, thereby reclaiming several activation frames in one go.
In C, non-local returns can be performed using the standard functions setjmp and longjmp, which can be seen as a form of goto that works across functions:
setjmp(b)saves its calling environment inb, and returns 0,longjmp(b,v)restores the environment stored inb, and proceeds like if the call tosetjmphad returnedvinstead of0.
Using extended trampolines, our example could be rewritten as follows, where we use _setjmp and _longjmp, which do not save and restore the signal mask and are therefore much more efficient.
typedef int (*fun_ptr)(int, int);
struct { fun_ptr fun; int arg; } resume;
jmp_buf jmp_env;
int even(int tcc, int x) {
if (tcc > TC_LIMIT) {
resume.fun = even;
resume.arg = x;
_longjmp(jmp_env, -1);
}
return (x == 0) ? 1 : odd(tcc + 1, x - 1);
}
int odd(int tcc, int x) { /* similar to even */ }
int main(int argc, char* argv[]) {
int res = (_setjmp(jmp_env) == 0)
? even(0, 300000000)
: (resume.fun)(0, resume.arg);
printf("%d\n",res);
}
5.4 Baker's technique
Baker's technique, due to Henry Baker, consists in first transforming the whole program to continuation-passing style (CPS). One important property of CPS is that all calls are tail calls. Consequently, it is possible to periodically shrink the whole stack using a non-local return. As above, this non-local return can be done using _setjmp / _longjmp in C.
Using Baker's technique, our example program would be:
typedef void (*cont)(int);
typedef void (*fun_ptr)(int, cont);
int tcc = 0;
struct { fun_ptr fun; int arg; cont k; } resume;
jmp_buf jmp_env;
void even_cps(int x, cont k) {
if (++tcc > TC_LIMIT) {
tcc = 0;
resume.fun = even_cps;
resume.arg = x;
resume.k = k;
_longjmp(jmp_env, -1);
}
if (x == 0) (*k)(1); else odd_cps(x - 1, k);
}
void odd_cps(int x, cont k) { /* similar to even_cps */ }
int main(int argc, char* argv[]) {
if (_setjmp(jmp_env) == 0) even_cps(300000000, main_1);
else (resume.fun)(resume.arg, resume.k);
}
void main_1(int val) { printf("%d\n", val); exit(0); }
5.5 Summary and benchmarks
The image below summarizes and compares the different techniques to perform tail call elimination in uncooperative environments that were described above. It shows how the stack of a program would evolve while executing the same program translated using each of them.

To have a (very basic) idea of how these techniques compare, the graph below shows the normalized running time of the programs presented above. Notice that these programs are extremely small and often very simplified compared to a full-fledged solution, and the results should therefore be taken with a grain of salt.

Notice that the initial version compiled without optimization produces a stack overflow, hence the absence of timing.