Memory management

1 Introduction

The memory of a computer is a finite resource. Typical programs use a lot of memory over their lifetime, but not all of it at the same time. The goal of memory management is to use that finite resource as efficiently as possible, according to some criterion.

In general, programs dynamically allocate memory from two different areas: the stack and the heap. Since the management of the stack is trivial, the term memory management usually designates that of the heap.

The memory manager is the part of the run time system in charge of managing heap memory. Its job consists in maintaining the set of free memory blocks (also called objects later) and to use them to fulfill allocation requests from the program.

2 Explicit vs implicit memory management

Memory allocation is generally explicit, in that the programmer chooses exactly when memory should be allocated.

On the other hand, memory deallocation can be either explicit or implicit:

it is explicit when the programmer asks for a block to be freed,
it is implicit when the memory manager automatically tries to free unused blocks at some point, e.g. when it does not have enough free memory to satisfy an allocation request.

Explicit memory deallocation presents several problems:

memory can be freed too early, which leads to dangling pointers — and then to data corruption, crashes, security issues, etc.
memory can be freed too late — or never — which leads to space leaks.

Due to these problems, most modern programming languages are designed to provide implicit deallocation, also called automatic memory management — or garbage collection, even though garbage collection refers to a specific kind of automatic memory management.

Implicit memory deallocation is based on the following conservative assumption: If a block of memory is reachable, then it will be used again in the future, and therefore it cannot be freed. Therefore, only unreachable memory blocks can be freed.

Since this assumption is conservative, it is possible to have memory leaks even with implicit memory deallocation. This happens whenever a reference to a memory block is kept, but the block is not accessed anymore. However, implicit deallocation completely eliminates dangling pointers.

Garbage collection (GC) is a common name for a set of techniques that automatically reclaim objects that are not reachable anymore. In the following, we will examine several garbage collection techniques:

reference counting,
mark and sweep,
copying, and
generational garbage collection.

3 Common concepts

Before looking at specific garbage collection techniques, we describe some concepts that are common to all of them.

3.1 Reachable objects

At any time during the execution of a program, we can define the set of reachable objects as being:

the objects immediately accessible from global variables, the stack or registers — called the roots or the root set, and
the objects reachable from other reachable objects, by following pointers.

These objects form the reachability graph, illustrated below for a very simple case where the root set consists only of four registers called R0 to R3.

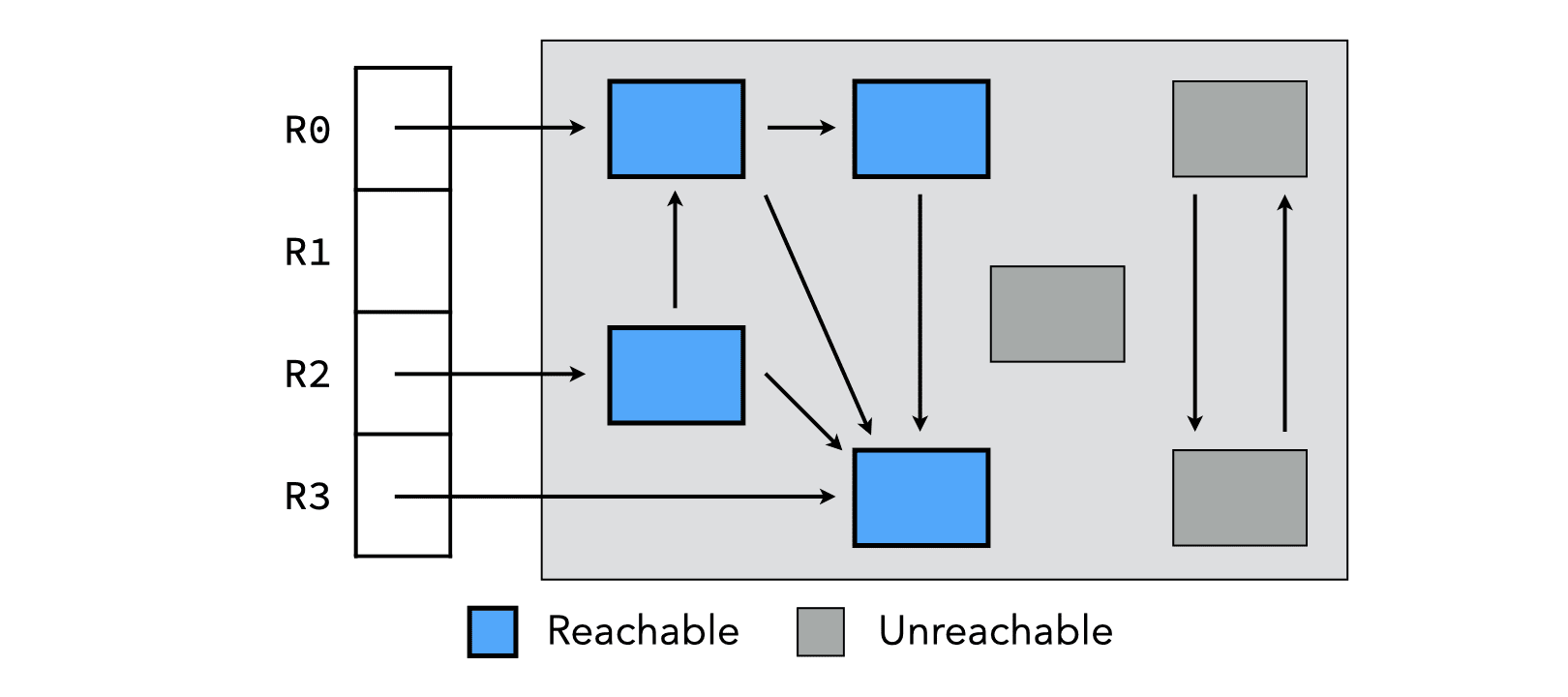
To compute the reachability graph at run time, it must be possible to unambiguously identify pointers in registers, in the stack, and in heap objects.

If this is not possible, the reachability graph must be approximated. Such an approximation must be safe for the task at hand. For example, when the reachability graph is used to free memory, it is only safe to over-approximate it.

3.2 Data structures

The memory manager must know which parts of the heap are free, and which are allocated. It typically does that by maintaining a collection of free blocks, called the free list. Despite its name, the free list is often not a simple list, its actual representation depends on the organization of the heap and the properties of the garbage collector.

The memory manager must associate a set of properties to the blocks it manages, for example their size. This is typically done by storing these properties in a block header, stored just before the area used by the program, as illustrated below:

To decrease the overhead of headers, the technique known as BiBoP (for big bag of pages) groups objects of identical size into contiguous areas of memory called pages. All pages have the same power-of-two size \(s = 2^b\) and start at an address which is a multiple of \(s\). The size of all the objects on a page is stored at the page's beginning, and can be retrieved by masking the \(b\) least-significant bits of an object's address.

3.3 Fragmentation

The term fragmentation is used to designate two different but similar problems associated with memory management:

external fragmentation refers to the fragmentation of free memory in many small blocks,
internal fragmentation refers to the waste of memory due to the use of a free block larger than required to satisfy an allocation request.

3.3.1 External fragmentation

The two heaps in the image below have the same amount of free memory, but the first suffers from external fragmentation. This means that the free memory is scattered over many non contiguous blocks. As a consequence, some allocation requests can be fulfilled by the second heap but not by the first.

3.3.2 Internal fragmentation

For various reasons — e.g. alignment constraints — the memory manager sometimes allocates slightly more memory than requested by the client. This results in small amounts of wasted memory scattered in the heap. This phenomenon is called internal fragmentation and is illustrated graphically below:

4 Reference counting GC

The first garbage collection technique we will examine is called reference counting.

Its idea is simple: every object carries, in its header, a count of the number of pointers that reference it. When this count reaches zero, the object is guaranteed to be unreachable and can be deallocated.

Notice that this technique requires collaboration from the compiler and/or the programmer, as the reference counts have to be properly maintained.

Reference counting is relatively easy to implement, even as a library, and it reclaims memory immediately. However, it has an important impact on space consumption, and speed of execution, as every object must contain a counter, and every pointer write must update it.

However, the major problem of reference counting is cyclic structures, since the reference count of objects that are part of a cycle in the object graph never reaches zero, even when they become unreachable, as illustrated in the following example:

This problem is due to the fact that reference counts provide only an approximation of reachability. In other words, we have:

reference count(x) = 0 ⇒ x is unreachable

but the opposite is not true!

Due to its problem with cyclic structures, reference counting is seldom used. It is still interesting for systems that do not allow cyclic structures to be created — e.g. hard links in Unix file systems. Besides, it has been used in combination with a mark and sweep GC, the latter being run infrequently to collect cyclic structures.

5 Mark and sweep GC

The second garbage collection technique we will examine is called mark and sweep.

As its name implies, it proceeds in two successive phases:

in the marking phase, the reachability graph is traversed and reachable objects are marked,
in the sweeping phase, all allocated objects are examined, and unmarked ones are freed.

GC is usually triggered by a lack of memory, and must complete before the program can be resumed. This is necessary to ensure that the reachability graph is not modified by the program while the GC traverses it.

An example animation of mark and sweep garbage collection is available in the lecture slides.

5.1 Allocation and deallocation

In a mark and sweep GC, free blocks are not contiguous in memory. As a consequence, allocation and deallocation are not trivial and deserve being discussed.

5.1.1 Free list

A mark and sweep GC stores the free blocks in a data structure usually known as the free list and which, in a simple GC, could actually be a simple linked list. Since the free blocks are, by definition, not used by the program, the links can be stored in the blocks themselves, as illustrated in the image below:

5.1.2 Allocation policy

When a block of memory is requested, there are in general many free blocks that are big enough to satisfy the request. An allocation policy must therefore be used to decide which of those candidates to choose. A good allocation policy should minimize fragmentation while being fast to implement.

The most commonly used policies are:

first fit, which uses the first suitable block,
best fit, which uses the smallest block big enough to satisfy the request.

5.1.3 Splitting and coalescing

When the memory manager has found a free block big enough to satisfy an allocation request, it is possible for that block to be bigger than the size requested. In that case, the block must be split in two parts: one part is returned to the client, while the other is put back into the free list.

The opposite must be done during deallocation: if the block being freed is adjacent to one or two other free blocks, then they all should be coalesced to form a bigger free block.

5.2 Marking phase

The marking phase is conceptuall simple, but two questions nevertheless have to be answered: how is the reachability graph traversed, and how are the objects marked?

5.2.1 Traversal

The marking phase requires a depth-first traversal of the reachabilty graph. This is usually implemented by recursion. Recursive function calls use stack space, and since the depth of the reachability graph is not bounded, the GC can overflow its stack!

Several techniques — not presented here — have been developed to either recover from those overflows, or avoid them altogether by storing the stack in the objects being traversed.

5.2.2 Marking

Reachable objects must be marked in some way. Since only one bit is required for the mark, it is possible to store it in the block header, along with the size. For example, if the system guarantees that all blocks have an even size, then the least significant bit (LSB) of the block size can be used for marking.

It is also possible to use "external" bit maps — stored in a memory area that is private to the GC — to store mark bits.

5.3 Sweeping phase

Once the marking phase has terminated, all allocated but unmarked objects can be freed. This is the job of the sweeping phase, which traverses the whole heap sequentially, looking for unmarked objects and adding them to the free list.

An example animation of the sweeping phase is available in the lecture slides.

Notice that unreachable objects cannot become reachable again. It is therefore possible to sweep objects on demand, to only fulfill the current memory need. This is called lazy sweep.

5.4 Conservative GC

A conservative mark and sweep garbage collector is one that is able to collect memory without unambiguously identify pointers at run time. This is possible because, for this kind of GC, an approximation of the reachability graph is sufficient to collect (some) garbage, as long as that approximation is a superset of the actual reachability graph.

A conservative GC assumes that everything that looks like a pointer to an allocated object is a pointer to an allocated object. This assumption is conservative — in that it can lead to the retention of dead objects — but safe — in that it cannot lead to the freeing of live objects.

It is however very important that the GC uses as many hints as possible to avoid considering non-pointers as pointers, as this can lead to memory being retained needlessly. Several characteristics of the architecture or compiler can be used to filter the set of potential pointers, e.g.:

Many architectures require pointers to be aligned in memory on 2 or 4 bytes boundaries. Therefore, unaligned potential pointers can be ignored.
Many compilers guarantee that if an object is reachable, then there exists at least one pointer to its beginning. Therefore, (potential) interior pointers can be ignored.

6 Copying GC

The third garbage collection technique we will examine is called copying garbage collection.

Its idea is to split the heap in two semi-spaces of equal size: the from-space and the to-space. Memory is allocated in from-space, while to-space is left empty. When from-space is full, all reachable objects in from-space are copied to to-space, and pointers to them are updated accordingly. Finally, the role of the two spaces is exchanged, and the program resumed.

An example animation of a copying garbage collector is available in the lecture slides.

6.1 Allocation

In a copying GC, memory is allocated linearly in from-space. There is no free list to maintain, and no search to perform in order to find a free block. All that is required is a pointer to the border between the allocated and free area of from-space. Allocation in a copying GC is therefore very fast — as fast as stack allocation.

6.2 Forwarding pointers

Before copying an object, a check must be made to see whether it has already been copied. If this is the case, it must not be copied again. Rather, the already-copied version must be used.

This can be done by storing a forwarding pointer in the object in from-space, after it has been copied. This pointer simply points to the copy of the object in to-space.

6.3 Cheney's algorithm

The copying GC algorithm presented above does a depth-first traversal of the reachabilty graph. When it is implemented using recursion, it can lead to stack overflow.

It is also possible to do a breadth-first traversal of the graph instead. In that case, the set of objects that have been visited but whose children haven't needs to be stored somewhere.

Cheney's algorithm uses an elegant technique to represent that set using only one additional pointer into to-space. This pointer, usually called scan, partitions the objects that have been copied into to-space in two: those whose children have been visited, and those whose children haven't been visited.

An example animation of a copying garbage collector using Cheney's algorithm is available in the lecture slides.

6.4 Mostly-copying GC

Unlike a mark and sweep GC, a copying GC cannot be conservative in general, as it needs to identify pointers unambiguously. Otherwise, when a value is mistaken for a pointer, it will be modified during GC, which is incorrect.

However, when most pointers can be identified unambiguously, it is possible to use a technique known as mostly-copying, due to Bartlett. The idea is to partition objects in two classes:

those for which some pointers are ambiguous, usually because they appear in the stack or registers,
those for which all pointers are known unambiguously.

Objects of the first class are pinned, i.e. left where they are, while the others — the vast majority, generally — are copied as usual.

Objects cannot be pinned if the from and to spaces are organized as two separate areas of memory, because from-space must be completely empty after GC. Therefore, a mostly-copying GC organizes memory in pages of fixed size, tagged with the space to which they belong. Then, during GC :

pinned objects are left on their page, whose tag is updated to "move" them to to-space,
other objects are copied (and compacted) as usual.

6.5 Pros and cons of copying GC

The table below presents the pros and cons of copying garbage collection, compared to mark and sweep.

Pros	Cons
no external fragmentation	uses twice as much (virtual) memory
very fast allocation	requires precise identification of pointers
no traversal of dead objects	copying can be expensive

7 Generational GC

The fourth garbage collection technique we will examine is known as generational garbage collection, and is not a separate technique but a refinement of copying or mark and sweep GC.

It is based on the empirical observation that a large majority of the objects die young, while a small minority lives for very long. Therefore, objects can be partitioned in generations — based on their age — and, the young generation(s) can be collected more often than the old one(s). This should improve the amount of memory collected per objects visited. In a copying GC, this also avoids repeatedly copying long-lived objects.

More precisely, objects are partitioned into a given number (often 2) of generations. The younger a generation is, the smaller the amount of memory reserved to it.

All objects are initially allocated in the youngest generation. When it is full, a minor collection is performed, to collect memory in that generation only. Some of the surviving objects are promoted to the next generation, based on a promotion policy. When an older generation is itself full, a major (or full) collection is performed to collect memory in that generation and all the younger ones.

An example animation of the minor collection of a generational copying GC is available in the lecture slides.

Notice that instead of managing all generations using a copying algorithm, it is also possible to manage some of them — the oldest, typically — using a mark and sweep algorithm.

7.1 Promotion policy

Generational GCs use a promotion policy to decide when objects should be advanced to an older generation.

The simplest one — all survivors are advanced — can promote very young objects, but is simple as object age does not need to be recorded. To avoid promoting very young objects it is sufficient to wait until they survive a second collection before advancing them.

To that end, the young generation can be split in three parts: a creation space (or Eden), a from-space and a to-space. All objects are allocated from the creation space, and during a minor collection, reachable objects are either moved to the youg to-space, or promoted to the old generation.

The various promotion policies and resulting heap organisations are presented graphically below:

7.2 Inter-generational pointers

The roots used for a minor collection must also include all pointers from older generations to younger ones. Otherwise, objects reachable only from the old generation would incorrectly get collected!

This is illustrated in the image below, where the highlighted pointer has to be taken into account during a minor collection, otherwise the object it points to would be considered unreachable.

Pointers from old to young generations, called inter-generational pointers, can be handled in two different ways:

by scanning — without collecting — older generations during a minor collection,
by detecting pointer writes using a write barrier — implemented either in software or through hardware support — and remembering inter-generational pointers.

The write barrier is a piece of code inserted by the compiler each time a pointer is overwritten, and whose goal is to track inter-generational pointers. Two techniques can be used to track them: remembered sets, and card marking.

7.2.1 Remembered set

The remembered set contains all objects that are old and that have at least one pointer to a young object. When a pointer is overwritten, the write barrier inserts the object that contains it into the remembered set if and only if:

the object is not yet in the set, and
the pointer is stored in an old object, and points to a young one — although this can also be checked later by the collector.

7.2.2 Card marking

Card marking is another technique to detect inter-generational pointers. Memory is divided into small, fixed sized areas called cards. A card table remembers, for each card, whether it potentially contains inter-generational pointers. On each pointer write, the card is marked in the table, and marked cards are scanned for inter-generational pointers during collection.

7.3 Nepotism

Since old generations are not collected as often as young ones, it is possible for dead old objects to prevent the collection of dead young objects. This problem is called nepotism and is illustrated in the image below, in which the highlighted pointer prevents the object it points to from being collected, despite the fact that it is actually unreachable.

7.4 Pros and cons of generational GC

Generational GC tends to reduce GC pause times since only the youngest generation, which is also the smallest and the one with the largest amount of dead objects, is collected most of the time. In copying GCs, the use of generations also avoids copying long-lived objects over and over.

The only problems of generational GCs are the cost of maintaining the remembered set and nepotism.

8 Other GC techniques

8.1 Incremental GC

An incremental garbage collector can collect memory in small, incremental steps, thereby reducing the length of GC pauses — a very important characteristic for interactive applications.

Incremental GCs must be able to deal with modifications to the reachability graph made by the main program — called the mutator — while they attempt to compute it. This is usually achieved using a write barrier that ensures that the reachability graph observed by the GC is a valid approximation of the real one.

Several techniques, not covered here, exist to guarantee the validity of this approximation.

8.2 Parallel GC

Some parts of garbage collection can be sped up considerably by performing them in parallel on several processors. This is becoming important with the popularization of multi-core architectures. For example, the marking phase of a mark and sweep GC can easily be done in parallel by several processors.

(Remember that parallelism and concurrency are separate and orthogonal concepts! A parallel GC does not have to be concurrent, and a concurrent GC does not have to be parallel.)

9 Additional GC features

The presence of a garbage collector makes it possible to add features based on it to the language. Two examples are given below.

9.1 Finalizers

Some GCs make it possible to associate finalizers with objects, which are functions that are called when an object is about to be collected. They are generally used to free "external" resources associated with the object about to be freed.

Since there is no guarantee about when finalizers are invoked, the resource in question should not be scarce.

Finalizers are tricky for a number of reasons:

what should be done if a finalizer makes the finalized object reachable again — e.g. by storing it in a global variable?
how do finalizers interact with concurrency — e.g. in which thread are they run?
how can they be implemented efficiently in a copying GC, which doesn't visit dead objects?

9.2 Weak references

When the GC encounters a reference, it usually treats it as a strong reference, meaning that the referenced object is considered as reachable and survives the collection. It is sometimes useful to have weaker kinds of references, which can refer to an object without preventing it from being collected.

The term weak reference (or weak pointer) designates a reference that does not prevent an object from being collected.

During a GC, if an object is only weakly reachable, it is collected, and all (weak) references referencing it are cleared. Weak references are useful to implement caches, "canonicalizing" mappings, etc.