Object-oriented languages

1 Introduction

Object-oriented languages offer several distinctive features that make their efficient implementation challenging, and which are the subject of this lesson.

2 Object-oriented languages

In a class-based object-oriented (OO) language, all values (or most of them) are objects, belonging to a class. Objects encapsulate both state, stored in fields, and behavior, defined by methods. (Prototype-based OO languages do not have a concept of class, but we will not cover them here.)

Two of the most important features of OO languages are inheritance and polymorphism, introduced below.

2.1 Inheritance

Inheritance is a code reuse mechanism that enables one class to inherit all fields and methods of another class, called its superclass. Inheritance is conceptually nothing but code copying (!), although it is usually implemented in a smarter way to prevent code explosion.

2.2 Subtyping

In typed OO languages, classes usually define types. These types are related to each other by a subtyping (or conformance) relation.

Intuitively, a type T₁ is a subtype of a type T₂ — written T₁ ⊑ T₂ — if T₁ has at least the capabilities of T₂.

When T₁ ⊑ T₂, a value of type T₁ can be used everywhere a value of type T₂ is expected. This ability to use a value of a subtype of T where a value of type T is expected is called inclusion polymorphism.

Inclusion polymorphism poses several interesting implementation challenges, by preventing the exact type of a value to be known at compilation time.

2.3 Inheritance vs subtyping

Inheritance and subtyping are not the same thing, but many OO languages tie them together by stating that:

every class defines a type, and
the type of a class is a subtype of the type(s) of its superclass(es).

This is a design choice, not an obligation!

Several languages also have a way to separate inheritance and subtyping in some cases. For example, Java interfaces make it possible to define subtypes that are not subclasses, while C++ has private inheritance that allows the definition of subclasses that are not subtypes.

The distinction between inheritance and subtyping is especially apparent in "dynamically typed" OO languages like Smalltalk, Ruby, Python, etc. In those languages, inheritance is used only to reuse code — no notion of (static) type even exists! Whether an object can be used in a given context only depends on the set of methods it implements, and not on the position of its class in the inheritance hierarchy.

2.4 Compilation challenges

When compiling object-oriented languages, the following problems are difficult to solve efficiently because of inclusion polymorphism:

object layout — arranging object fields in memory,
method dispatch — finding which concrete implementation of a method to call,
membership tests — testing whether an object is an instance of some type.

We examine each one in turn below.

3 Object layout

The object layout problem consists in finding how to arrange the fields of an object in memory so that they can be accessed efficiently.

Inclusion polymorphism makes the problem hard because it forces the layout of different object types to be compatible in some way. Ideally, a field defined in a type T should appear at the same offset in all subtypes of T. That way, it can be accessed very efficiently.

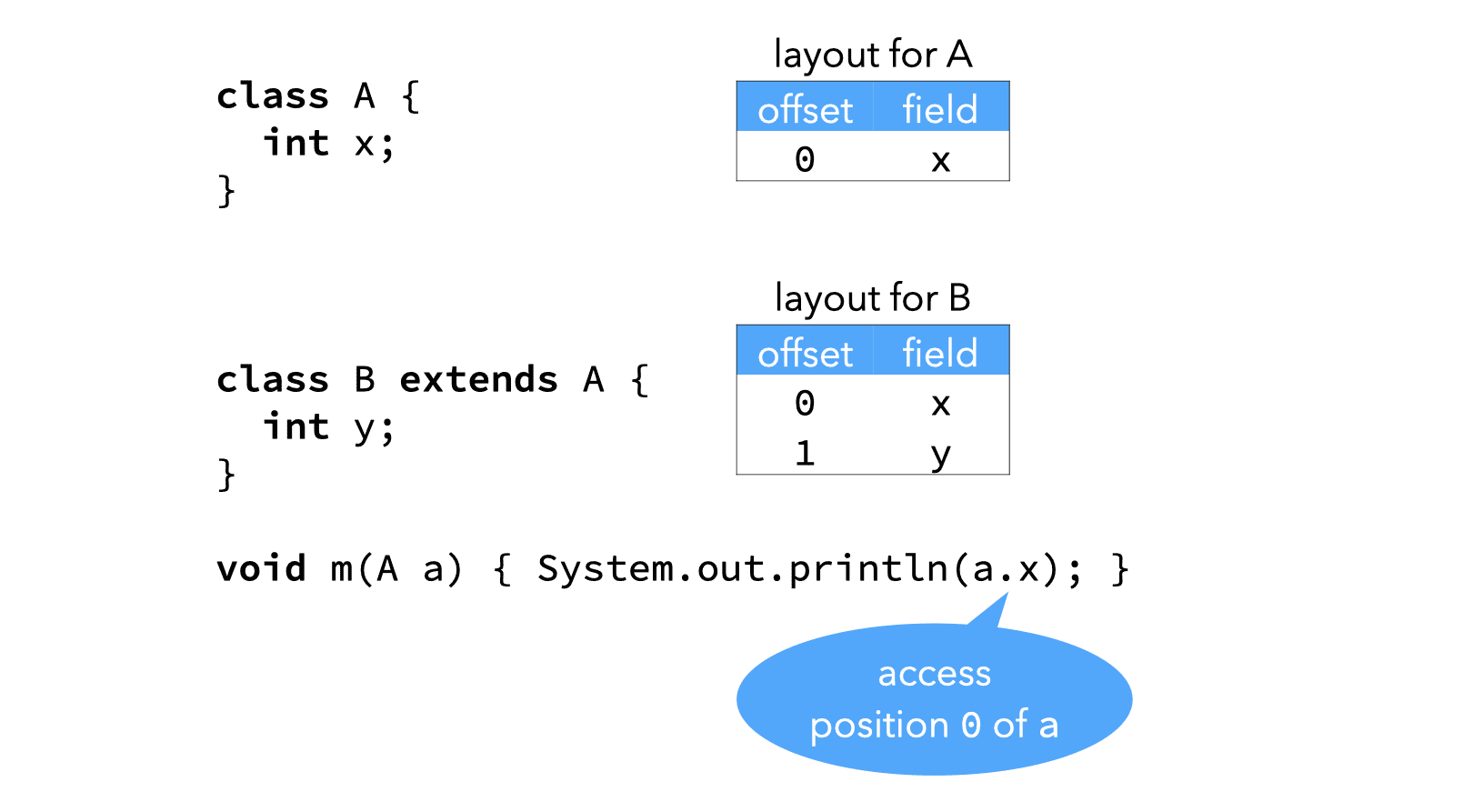
Consider for example the following simple Java hierarchy:

class A {
  int x;
}
class B extends A {
  int y;
}

and the following method, appearing in some unspecified class:

void m(A a) {
  // Q: at which position does x appear?
  System.out.println(a.x);
}

It is not possible to know at compilation time the actual type of the object a passed to m, which could be A or B. Therefore, unless field x appears at the same position in instances of A and in instances of B, it is not trivial to generate efficient code to extract it.

3.1 Case 1: single inheritance

In single-inheritance languages where subtyping and inheritance are tied (e.g. Java), the object layout problem can be solved easily as follows:

The fields of a class are laid out sequentially, starting with those of the superclass — if any.

This ensures that all fields belonging to a type T₁ appear at the same location in all values of type T₂ ⊑ T₁.

For the example above, this implies that instances of A and B are laid out as illustrated below:

3.2 Case 2: multiple inheritance

In a multiple inheritance setting, the object layout problem becomes much more difficult. For example, in the following hierarchy, how should fields be laid out?

If a standard, unidirectional layout is used, then some space is wasted:

Other solutions therefore have to be found.

3.2.1 Bidirectional layouts

For the example hierarchy above, it is possible to use a bidirectional layout to avoid wasting space. In such a layout, some fields are put at negative indices, like y below:

Unfortunately, there does not always exist a bidirectional layout that does not waste space. Moreover, finding an optimal bidirectional layout — one minimizing the wasted space — has been shown to be NP-complete.

Finally, computing a good bidirectional layout requires the whole hierarchy to be known! It must be done at link time, and is not really compatible with Java-style run time linking.

3.2.2 Accessor methods

Another way of solving the object layout problem in a multiple inheritance setting is to always use accessor methods to read and write fields.

The fields of a class can then be laid out freely. Whenever the offset of a field is not the same as in the superclass from which it is inherited, the corresponding accessor method(s) are redefined.

This reduces the object layout problem to the method dispatch problem, which we will examine later.

3.2.3 Other techniques

Bidirectional layout often wastes space, but field access is extremely fast. Accessor methods never waste space, but slow down field access.

Two-dimensional bidirectional layout slows down field access slightly — compared to bidirectional layout — but never wastes space. However, it also requires the full hierarchy to be known. We will not examine it here.

3.3 Summary

The object layout problem can be solved trivially in a single-inheritance setting, by laying out the fields sequentially, starting with those of the superclass.

In a multiple-inheritance setting, solutions to that problem are more complicated, and must generally trade space for speed, or speed for space. They also typically require the whole hierarchy to be known in advance.

4 Method dispatch

The method dispatch problem consists in finding, given an object and a method identity, the exact piece of code to execute.

Inclusion polymorphism makes the problem hard since it prevents the problem to be solved statically — i.e. at compilation time. Efficient dynamic dispatching methods therefore have to be devised.

This is illustrated by the Java example below, where the exact implementation of the method m that has to be invoked from f cannot be known at compilation time, and therefore has to be determined at run time, as efficiently as possible.

class A {
  int x;
  void m() { println("m in A"); }
  void n() { println("n in A"); }
}
class B extends A {
  int y;
  void m() { println("m in B"); }
  void o() { println("o in B"); }
}
void f(A a) {
  // Q: which implementation of m should be invoked?
  a.m();
}

4.1 Case 1: single subtyping

In single-inheritance languages where subtyping and inheritance are tied, the method dispatch problem can be solved easily as follows:

Method pointers are stored sequentially, starting with those of the superclass, in a virtual methods table (VMT) shared by all instances of the class.

This ensures that the implementation for a given method is always at the same position in the VMT, and can be extracted quickly.

The image below illustrates how the VMTs of three instances of the classes A and B presented above would be organized.

Using a VMT, dispatching is accomplished in three steps:

the VMT of the receiver is extracted,
the code pointer for the invoked method is extracted from the VMT,
the method implementation is invoked.

Each of these steps typically requires a single — but expensive — instruction on modern CPUs.

VMTs provide very efficient dispatching, and do not use much memory. They work even in languages like Java where new classes can be added to the bottom of the hierarchy at run time. Unfortunately, they do not work for dynamic languages or in the presence of any kind of "multiple subtyping" — e.g. multiple interface inheritance in Java.

4.2 Case 2: multiple subtyping

To understand why VMTs cannot be used with multiple subtyping, consider the following Java interface:

interface Drawable {
  void draw();
}

and the following method iterating over a list of objects implementing that interface to invoke their draw method:

void drawAll(List<Drawable> ds) {
  for (Drawable d: ds)
    d.draw();
}

When the draw method is invoked, the only thing known about d is that it has a draw method — but nothing is known about its class, which be anywhere in the hierarchy!

For example, in the following hierarchy, the method draw appears at different positions in the VMTs of instances of Shape and instances of Window.

4.2.1 Dispatching matrix

A trivial way to solve the problem is to use a global dispatching matrix, containing code pointers and indexed by classes and methods.

For the above hierarchy, the dispatching matrix would look as follows:

The dispatching matrix makes dispatching very fast. However, for any non-trivial hierarchy, it occupies so much memory that it is never used as-is in practice. Instead, it is compressed using techniques that save space while still allowing efficient dispatch. These techniques take advantage of two characteristics of the dispatching matrix:

it is sparse, since in a large program any given class implements only a limited subset of all methods,
it contains a lot of redundancy, since many methods are inherited.

4.2.2 Null elimination

The dispatching matrix is very sparse in practice. Even in our trivial example, about 50% of its slots are empty.

A first technique to compress the matrix is therefore to take advantage of this sparsity. This is called null elimination, since the empty slots of the matrix usually contain null.

The only null elimination technique that we will examine is called column displacement. It consists in transforming the matrix into a linear array by shifting its columns. Many holes of the matrix can be filled while doing so, by carefully choosing the amount by which columns are shifted.

Instead of columns, it is also possible to shift rows, but column displacement produces better results in practice. On our example, column displacement manages to eliminate all unused space in the matrix, but this is due to the fact that this example is simple:

Dispatching with column displacement consists in:

adding the offset of the method being invoked — known at compilation time — to the offset of the class of the receptor — known only at run time — to extract the code pointer,
invoking the method referenced by that pointer.

It is therefore as fast as dispatching with an uncompressed matrix.

4.2.3 Duplicates elimination

Apart from being sparse, the dispatching matrix also contains a lot of duplicated information. Null elimination does not take advantage of this duplication, and even though it achieves good compression, it is possible to do better.

The idea of duplicates elimination techniques is to try to share as much information as possible instead of duplicating it. Compact dispatch tables are such a technique.

The idea of compact dispatch tables is to split the dispatch matrix into small sub-matrices called chunks. Each individual chunk will tend to have duplicate rows, which can be shared by representing each chunk as an array of pointers to rows.

Dispatching with a compact dispatch table consists in:

combining the offset and chunk of the method being invoked — known at compilation time — with the index of the receiver — known only at run time — to extract the code pointer,
invoking the method referenced by that pointer.

Because of the additional indirection due to the chunk array, this technique is slightly slower than column/row displacement. However, it tends to compress the dispatching matrix better in practice.

4.2.4 Hybrid techniques

VMTs and the more sophisticated techniques handling multiple subtyping are not exclusive.

For example, all Java implementations use VMTs to dispatch when the type of the receiver is a class type, and more sophisticated — and slower — techniques when it is an interface type. The JVM even has different instructions for the two kinds of dispatch: invokevirtual and invokeinterface.

4.3 Method dispatch optimization

Even when efficient dispatching structures are used, the cost of performing a dispatch on every method call can become important.

In practice, it turns out that many calls that are potentially polymorphic are in fact monomorphic, that is they target a single implementation of the method.

The idea of inline caching is to take advantage of this fact by recording — at every call site — the target of the latest dispatch, and assuming that the next one will be the same.

4.3.1 Inline caching

Inline caching works by patching code: At first, all method calls are compiled to call a standard dispatching function. Whenever this function is invoked, it computes the target of the call, and then patches the original call to refer to the computed target.

All methods have to handle the potential mispredictions of this technique, and invoke the dispatching function when they happen.

The image below shows how inline caching works when a list of five objects of type Drawable (three instances of Circle, followed by two of Rectangle) is iterated over, and the draw method of each object is invoked.

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

Inline caching greatly speeds up method calls by avoiding expensive dispatches in most cases. However, it can also slow down method calls that are really polymorphic! For example, if the list ds above contained an alternating sequence of circles and rectangles.

Polymorphic inline caching addresses this issue.

4.3.2 Polymorphic inline caching

Inline caching replaces the call to the dispatch function by a call to the latest method that was dispatched to.

Polymorphic inline caching (PIC) replaces it instead by a call to a specialized dispatch routine, generated on the fly. That routine handles only a subset of the possible receiver types — namely those that were encountered previously at that call site.

Polymorphic inline caching is illustrated below, which is similar to the previous one except that the elements of the list are alternatively instances of Circle and instances of Rectangle.

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

The specialized dispatch function must be able to test very quickly whether an object is of a given type. This can be accomplished for example by storing a tag in every object, representing its class.

It must be noted that this test does not check whether the type of the receiver is a subtype of a given type, but whether it is equal to a given type. This implies that several entries in the specialized dispatch function can actually call the same method, if that method is inherited.

An interesting feature of PIC is that the methods called from the specialized dispatch function can be inlined into it, provided they are small enough. For example, PIC_d2 could become:

if rectangle
  // inlined code of drawR
else if circle
  // inlined code of drawC
else
  dispatch

Moreover, the tests can be rearranged so that the ones corresponding to the most frequent receiver types appear first.

4.4 Summary

The method dispatch problem is solved by virtual method tables in a "single subtyping" context.

In presence of multiple subtyping, some compressed form of a global dispatching matrix is used. Compression techniques take advantage of the sparsity and redundancy of that matrix.

Inline caching and its polymorphic variant can dramatically reduce the cost of dispatching.

5 Membership test

The membership test problem consists in checking whether an object belongs to a given type.

This problem must be solved very often. In Java, for example, a membership test must be done on every use of the instanceof operator, type cast or array store operation, and every time an exception is thrown — to identify the matching handler.

The following Java example illustrates one situation in which this problem must be solved:

class A { }
class B extends A { }
boolean f(Object o) {
  // Q: is o an instance of A or any of its subtypes?
  return (o instanceof A);
}

5.1 Case 1: single subtyping

Like the other two problems we examined, the membership test is relatively easy to solve in a single subtyping setting. We will examine two techniques that work in that context:

relative numbering, and
Cohen's encoding.

5.1.1 Relative numbering

The idea of relative numbering is to number the types in the hierarchy during a preorder traversal.

This numbering has the important characteristic that the numbers attributed to all descendants of a given type are contiguous. Membership tests can therefore be performed very efficiently, by checking whether the number attributed to the type of the object being tested belongs to a given interval.

This is illustrated for a tiny subset of the Java hierarchy below:

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

5.1.2 Cohen's encoding

The idea of Cohen's encoding is to first partition the types according to their level in the hierarchy. Then, all types are numbered so that no two types at a given level have the same number. Finally, a display is attached to all types T, mapping all levels L smaller or equal to that of T to the number of the ancestor of T at level L.

(The level of a type T is defined as the length of the path from the root to T.)

Cohen's encoding is illustrated below on the same hierarchy as the one used above:

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

Cohen's encoding can be optimized further by using globally-unique identifiers for types, instead of level-unique ones. In that case, the display bounds check can be removed if the displays are stored consecutively in memory, with the longest ones at the end.

This optimized variant is presented graphically below for the first three levels of our example hierarchy:

5.1.3 Relative numbering vs Cohen's encoding

While Cohen's encoding is more complex and requires more memory than relative numbering, it has the advantage of being incremental. That is, it is possible to add new types to the hierarchy without having to recompute all the information attached to types. This characteristic is important for systems where new types can be added at run time, e.g. Java.

5.2 Case 2: multiple subtyping

In a multiple subtyping setting, neither relative numbering nor Cohen's encoding can be used directly. Techniques that work with multiple subtyping can however be derived from them. We will briefly describe three of them:

range compression,
packed encoding, and
PQ encoding.

5.2.1 Range compression

Range compression is a generalization of relative numbering to a multiple subtyping setting.

The idea of this technique is to uniquely number all types of the hierarchy by traversing one of its spanning forests — chosen judiciously. Then, each type carries the numbers of all its descendants, represented as a list of disjoint intervals.

Range compression is illustrated below on a hierarchy composed of 9 types named A to I. The arrows represent the subtyping relation, and the red ones show the chosen spanning forest.

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

5.2.2 Packed encoding

Packed encoding is a generalization of Cohen's encoding to a multiple inheritance setting.

The idea of this technique is to partition types into slices — as few as possible — so that all ancestors of all types are in different slices. Types are then numbered uniquely in all slices. Finally, a display is attached to every type T, mapping slices to the ancestor of T in that slice.

Packed encoding is illustrated on the same hierarchy as before in the image below, where the colors represent the slices:

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

It is easy to see that Cohen's encoding is a special case of packed encoding, in which levels play the role of slices. In a single inheritance setting, it is always valid to use levels as slices, since it is impossible for a type to have two ancestors at the same level — i.e. in the same slice.

5.2.3 PQ encoding

PQ encoding borrows ideas from packed encoding and relative numbering.

It partitions types into slices — as few as possible — and attributes to types one unique identity per slice. The numbering of types is done so that the following property holds:

For all types T in a slice S, all descendants of T — independently of their slice — are numbered consecutively in slice S.

PQ encoding is illustrated on the same hierarchy as before in the image below, in which classes are colored according to the slice to which they belong. In this case, one slice is enough:

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

If an additional type J is added to the hierarchy as illustrated below, a second slice becomes necessary:

(This image is also available in the lecture slides as an animation, which might be easier to understand.)

5.2.4 Hybrid techniques

Like for the dispatch problem, it is perfectly possible to combine several solutions to the membership test problem.

For example, a Java implementation could use Cohen's encoding to handle membership tests for classes, and PQ encoding for interfaces.

5.3 Summary

In a single subtyping context, two simple solutions to the membership test exist: relative numbering and Cohen's encoding. Only the latter is incremental, in that it supports the incremental addition of types at the bottom of the hierarchy.

Generalizations of these techniques exist for multiple subtyping contexts: range compression, packed and PQ encoding. Those techniques enable the membership test to be solved efficiently, but the building of the supporting data structures is relatively complicated. Moreover, they require the whole hierarchy to be available, and are not incremental.